Marie-Charlotte Brandenburg | Hyperplane Sections of Polytopes

Affine Sections of Polytopes
Intersection Bodies of Polytopes
- Supplementary Material (including a gallery of 3d models)

Affine Sections of Polytopes

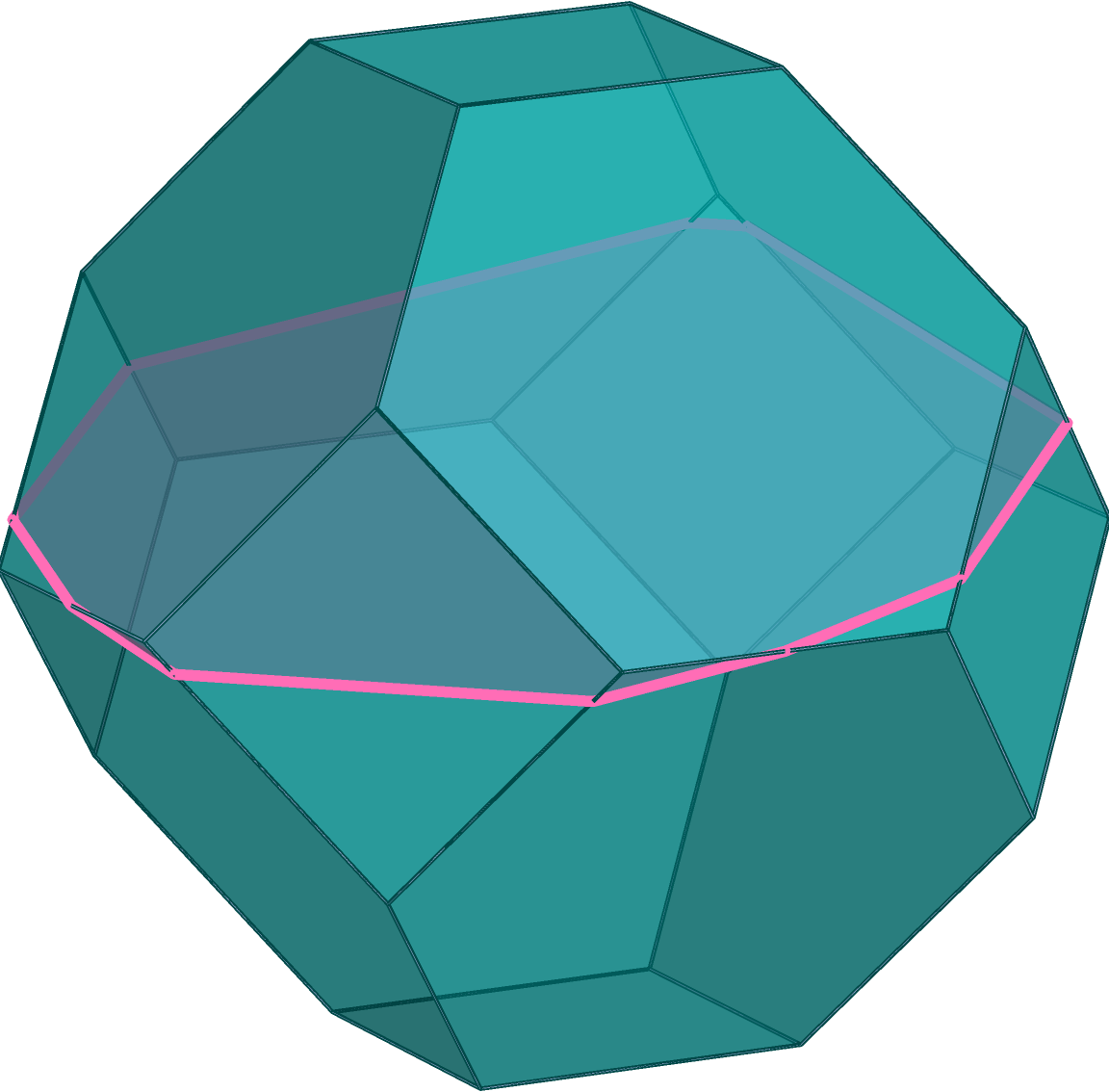
Given a 3-dimensional cube, the intersection with an affine hyperplane is always a polygon with 3,4,5, or 6 vertices. But how can one understand the slices of a general polytope? And which slice is “the best,” e.g., is the slice of maximal volume?

In [BDLM24] we study the structure of the set of all possible sections of a convex polytope by arbitrary affine hyperplanes. We encounter several subdivisions of the space of hyperplanes into polyhedral cells with the property that all hyperplane sections coming from the same cell form a class of equivalent polytopes. Computing all such classes of hyperplanes allows for the identification of the optimal section according to numerous possible combinatorial criteria.

In each of these polyhedral cells, the volume of the hyperplane section can be expressed as a rational function, a quotient of two polynomials, in the parameters identifying the hyperplane. Finding the section of maximum volume thus turns into a global optimization problem over all polyhedral cells. With analogous strategies, one can extend these results further from hyperplane sections to orthogonal projections onto hyperplanes, and intersections with affine half-spaces.

In the article, we describe two approaches, which we call the rotational and the translational approach. In the rotational approach, we first choose the position of the origin, which induces the cocircuit arrangement \(\mathcal{R}_{\circlearrowleft}\). Once we have fixed the origin, we consider central sections, i.e. intersections with hyperplane through the origin. This induces a second hyperplane arrangement \(\mathcal{C}_{\circlearrowleft}\). Here is an animation which illustrates the interaction between these two arrangements for a fixed pentagon (grey polygon on the right side). The left picture shows the space of translation vectors, and black dot in the left picture represents a translation vector \(t\) of the polytope \(P\), and thus determines the position of the origin. The right picture shows the polytope (grey pentagon in the left picture), and the black dot in the right picture represents the origin.

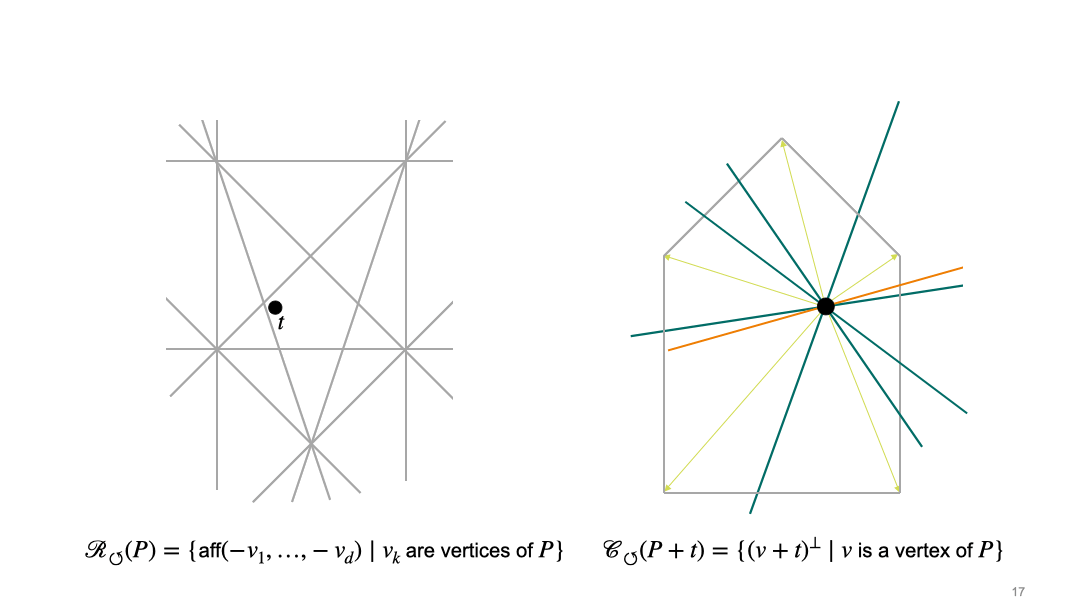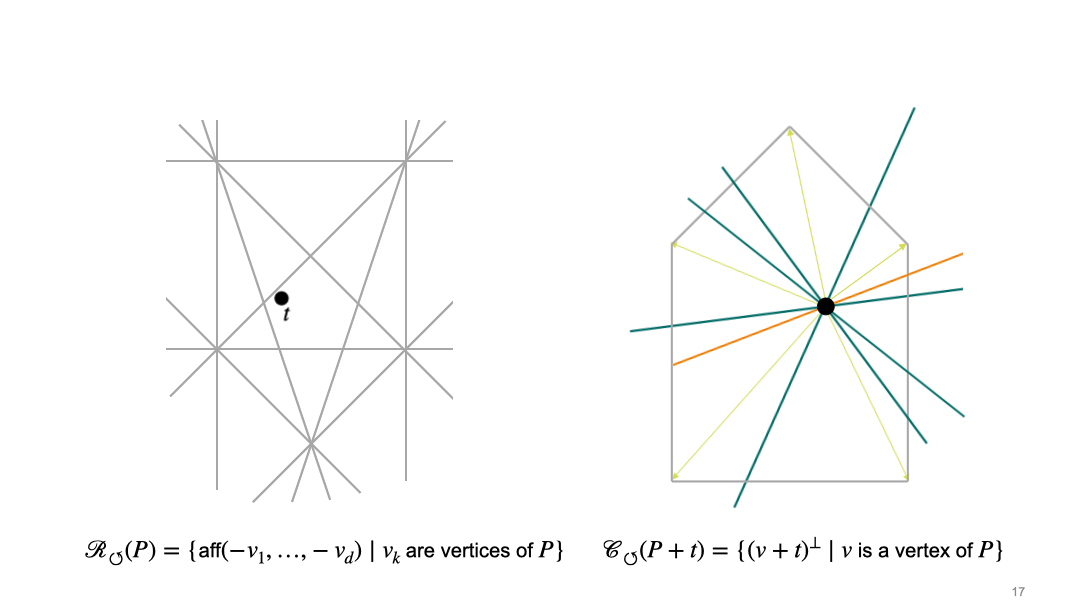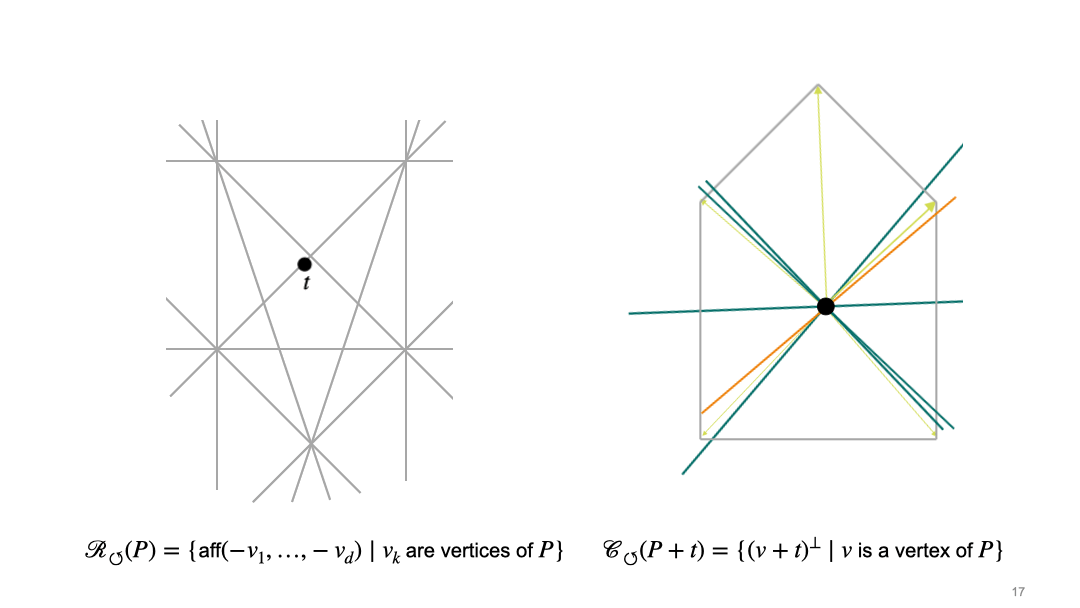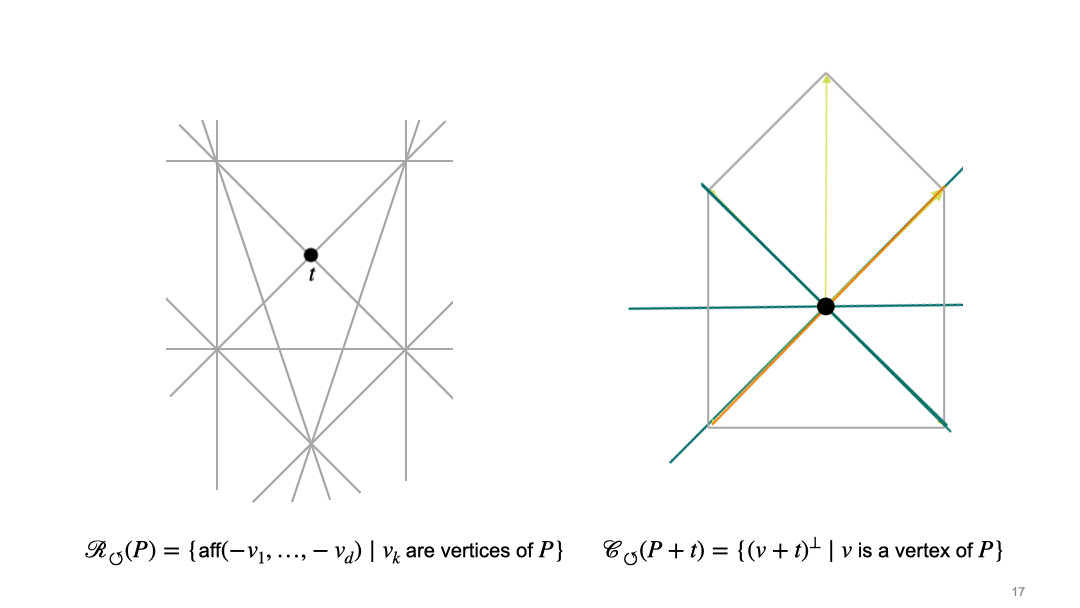
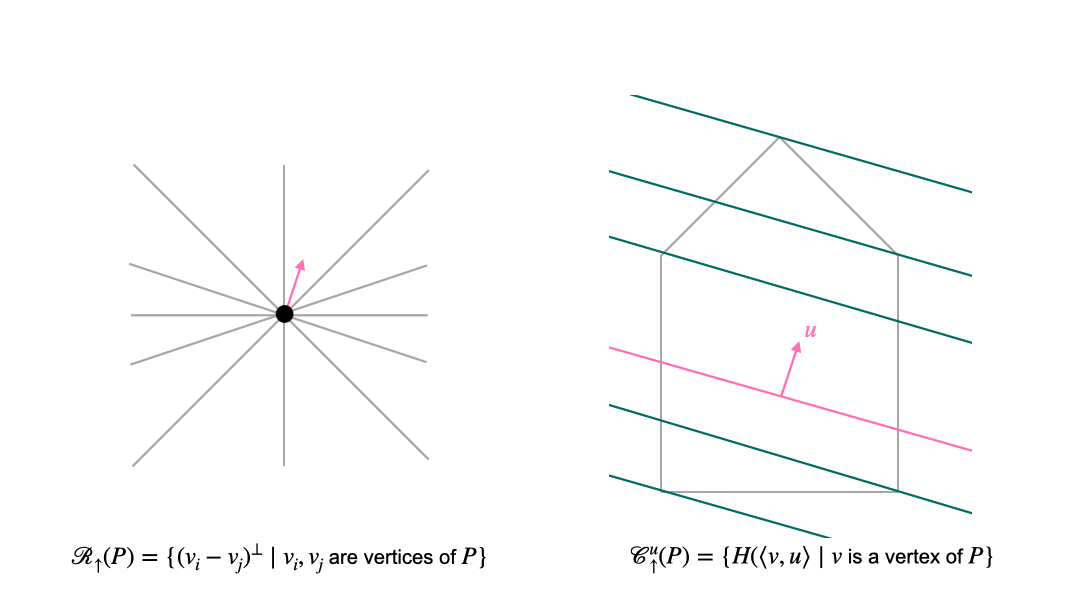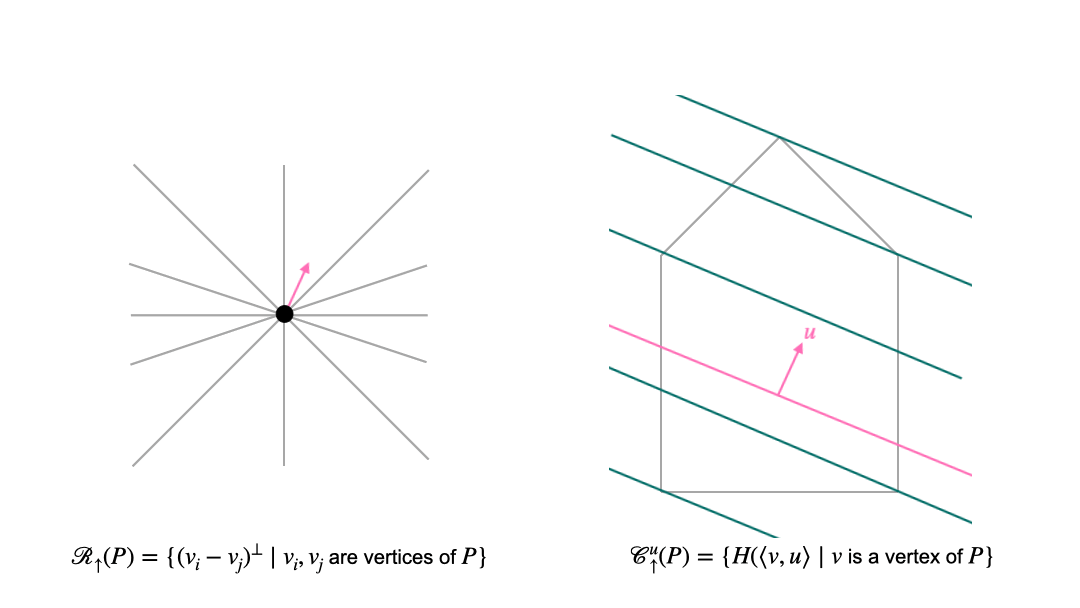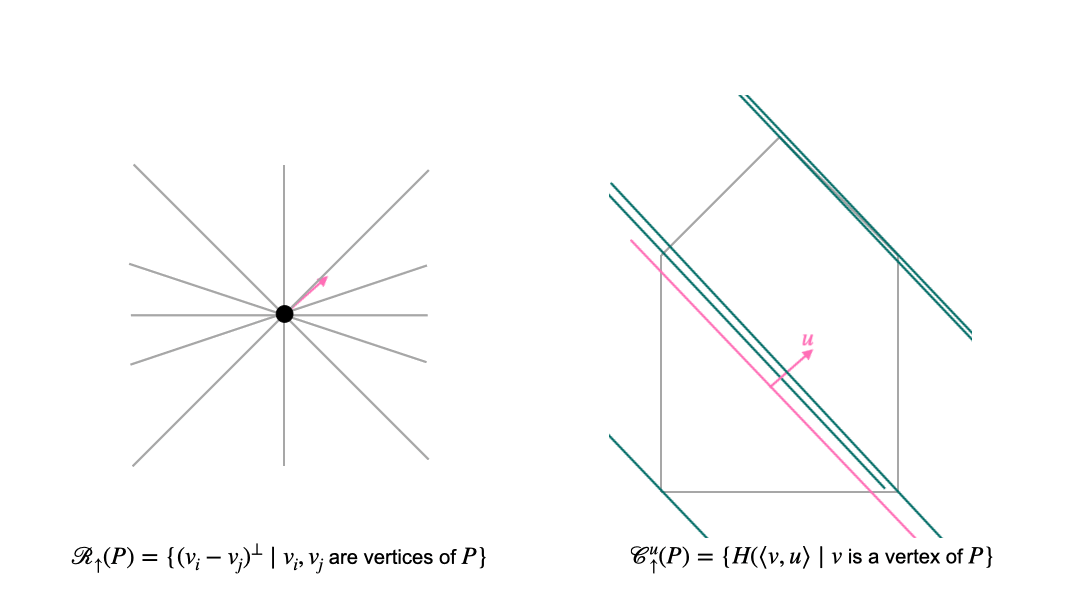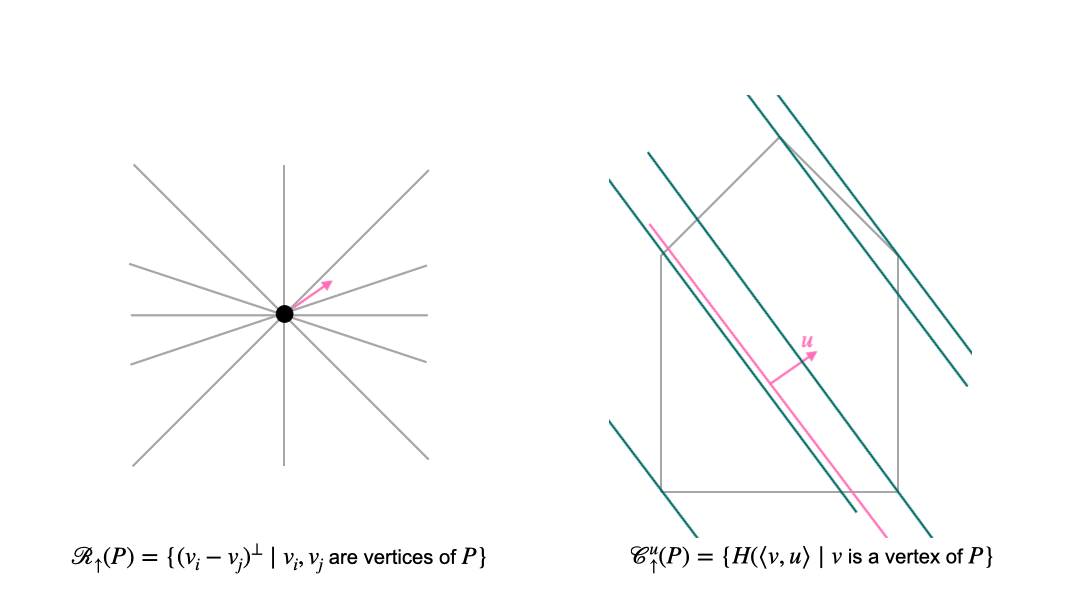
rotational approach

In the translational approach, we first choose a normal direction. These directions are organized by the sweep arrangement (or lineup arrangement) \(\mathcal{R}_{\uparrow}\). Once we have fixed the normal direction, we consider intersections of the polytope with affine translates of the hyperplane that is orthogonal to the chosen normal vector. These affine hyperplanes can be organized into chambers of the parallel arrangement \(\mathcal {C}_{\uparrow}\). The following animation shows the interplay between the two arrangement in the translational approach. The left picture shows the space of normal vectors, and the right picture shows the polytope (grey pentagon) and affine hyperplanes which are orthogonal to the normal vector \(u\) (pink).

rotational approach

References

The Best Ways to Slice a Polytope with Jesús A. de Loera, and Chiara Meroni. Mathematics of Computation, 2024. [abstract] [doi] [arXiv] [supplementary material] [bibtex]
We study the structure of the set of all possible affine hyperplane sections of a convex polytope. We present two different cell decompositions of this set, induced by hyperplane arrangements. Using our decomposition, we bound the number of possible combinatorial types of sections and craft algorithms that compute optimal sections of the polytope according to various combinatorial and metric criteria, including sections that maximize the number of \(k\)-dimensional faces, maximize the volume, and maximize the integral of a polynomial. Our optimization algorithms run in polynomial time in fixed dimension, but the same problems show hardness otherwise. Our tools can be extended to intersection with halfspaces and projections onto hyperplanes. Finally, we present several experiments illustrating our theorems and algorithms on famous polytopes.
```
@article{bdlm24,
  title = {The Best Ways to Slice a Polytope},
  author = {Brandenburg, Marie-Charlotte and {de Loera}, Jes\'us A. and Meroni, Chiara},
  journal = {Mathematics of Computation},
  year = {2024},
  doi = {10.1090/mcom/4006}
}
```

NSF Research Highlight: Slices of Polytopes with Chiara Meroni. March 2023. [url]

Slides of Talks


13 March 2024	Combinatorics Seminar at KTH in Stockholm	[Slides]
23 November 2023	Discrete Geometry Seminar at FU Berlin	[Slides]
05 June 2023	Nonlinear Algebra Seminar at MPI MiS in Leipzig	[Slides]

Intersection Bodies of Polytopes

Intersection bodies of polytopes are geometric objects, which we can describe by using a variety of combinatorial and algebraic methods. The intersection body of a geometric object is constructed by measuring the volume of central hyperplane sections. More precisely, let \(P \subseteq \mathbb{R}^d\) be a star body (for example a convex body or a polytope). Pick a unit direction \(u \in S^{d-1}\) on the unit sphere, and let \(u^\perp \subseteq \mathbb{R}^d\) denote the orthogonal hyperplane contiaining the origin. We measure the \((d-1)\)-dimensional Euclidean volume \(\rho(u)\) of the section \(P \cap u^\perp\). The intersection body \(IP\) of \(P\) is defined to be the unique star body such that \(\rho(u)\) is the distance from the origin to the boundary of \(IP\) in direction \(u\). This video illustrates this construction:

(To show this video in full-screen click here)

Historically, intersection bodies arose from questions in convex analysis, and have thus mostly been studied with methods drawn from this area. They are closely related projection bodies and cross-section bodies. Richard Garnder has coined the term Geometric Tomography for the study of these objects, which he describes as “the area of mathematics dealing with the retrieval of information about a geometric object from data about its sections, or projections, or both.”

In general, intersection bodies are not semialgebraic sets. However, in the case of polytopes, we show that the intersection body of a polytope is always semialgebraic, and we provide an algorithm for its computation [BBMS22]. We show that the regions of polynomiality of the boundary of \(IP\) are defined by a hyperplane arrangement, which allows us to associate a zonotope to an intersection body of a polytope.
Furthermore, we consider the algebraic boundary of \(IP\), which is the algebraic variety that is the (complex) Zariski closure of its Euclidean boundary. We compute the irreducible components of the algebraic boundary and provide an upper bound for the degree of these components.

Although intersection bodies of polytopes inherit some of the combinatorial structures of the polytopes, they are not always convex sets. In fact, it is known that every star body has an affine translation such that its intersection body is non-convex. In the second article [BM24], we consider the behaviour of an intersection body of a polytope when translating the polytope and pose the following question:

For a fixed polytope \(P\), what is the set of translations \(t\) such that the intersection body \(I(P+t)\) of \(P+t\) is convex?

Surprisingly, it turns out that the intersection body of a polygon is convex if and only if the polygon is centrally symmetric and centered at the origin. Whe show that the same statement can be made for cubes of arbitrary dimensions, but not for general polytopes.

Slides of Talks


23 March 2022	Combinatorial Coworkingspace	[Slides]
14 February 2022	Colloquium of Facets of Complexity in Berlin	[Slides]
30 November 2021	Women in Algebra and Symbolic Computation II	[Slides]
18 November 2021	Nonlinear Algebra Seminar at MPI MiS in Leipzig	[Slides]

References

Intersection Bodies of Polytopes: Translations and Convexity with Chiara Meroni. Journal of Algebraic Combinatorics, May 2024. [abstract] [doi] [bibtex]
We continue the study of intersection bodies of polytopes, focusing on the behavior of \(IP\) under translations of \(P\). We introduce an affine hyperplane arrangement and show that the polynomials describing the boundary of \(I(P+t)\) can be extended to polynomials in variables \(t ∈R^d\) within each region of the arrangement. In dimension 2, we give a full characterization of those polygons such that their intersection body is convex. We give a partial characterization for general dimensions.
```
@article{bm24,
  title = {Intersection Bodies of Polytopes: Translations and Convexity},
  author = {Brandenburg, Marie-Charlotte and Meroni, Chiara},
  year = {2024},
  month = may,
  journal = {Journal of Algebraic Combinatorics},
  doi = {10.1007/s10801-024-01328-9}
}
```
Intersection Bodies of Polytopes with Katalin Berlow, Chiara Meroni, and Isabelle Shankar. Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry, 63(2):419–439, June 2022. [abstract] [doi] [supplementary material] [bibtex]
We investigate the intersection body of a convex polytope using tools from combinatorics and real algebraic geometry. In particular, we show that the intersection body of a polytope is always a semialgebraic set and provide an algorithm for its computation. Moreover, we compute the irreducible components of the algebraic boundary and provide an upper bound for the degree of these components.
```
@article{bbms22,
  title = {Intersection Bodies of Polytopes},
  author = {Berlow, Katalin and Brandenburg, Marie-Charlotte and Meroni, Chiara and Shankar, Isabelle},
  year = {2022},
  month = jun,
  journal = {Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry},
  volume = {63},
  number = {2},
  pages = {419--439},
  doi = {10.1007/s13366-022-00621-7}
}
```

Supplementary Material

Gallery of 3D models
Click here for a gallery of intersection bodies of translates of the 3-dimensional cube.

MathRepo
Our MathRepo page contains additional supplementary material:

We implemented an algorithm in SageMath to compute interseciton bodies of polytopes of any dimension. We also implemented this algorimth in OSCAR for polytopes of dimension at most 3
We provide a step by step explanation of the algorithm with the example of the cube