publications

2024

1. 

   Quotients of M-convex sets and M-convex functions with Georg Loho, and Ben Smith. 2024. [abstract] [arXiv]

   We unify the study of quotients of matroids, polymatroids, valuated matroids and strong maps of submodular functions in the framework of Murota’s discrete convex analysis. As a main result, we compile a list of ten equivalent characterizations of quotients for M-convex sets, generalizing existing formulations for (poly)matroids and submodular functions. We also initiate the study of quotients of M-convex functions, constructing a hierarchy of four separate characterizations. Our investigations yield new insights into the fundamental operation of induction, as well as the structure of linking sets and linking functions, which are generalizations of linking systems and bimatroids.

2. 

   Decomposition Polyhedra of Piecewise Linear Functions with Moritz Grillo, and Christoph Hertrich. 2024. [abstract] [arXiv]

   In this paper we contribute to the frequently studied question of how to decompose a continuous piecewise linear (CPWL) function into a difference of two convex CPWL functions. Every CPWL function has infinitely many such decompositions, but for applications in optimization and neural network theory, it is crucial to find decompositions with as few linear pieces as possible. This is a highly challenging problem, as we further demonstrate by disproving a recently proposed approach by Tran and Wang [Minimal representations of tropical rational functions. Algebraic Statistics, 15(1):27-59, 2024]. To make the problem more tractable, we propose to fix an underlying polyhedral complex determining the possible locus of nonlinearity. Under this assumption, we prove that the set of decompositions forms a polyhedron that arises as intersection of two translated cones. We prove that irreducible decompositions correspond to the bounded faces of this polyhedron and minimal solutions must be vertices. We then identify cases with a unique minimal decomposition, and illustrate how our insights have consequences in the theory of submodular functions. Finally, we improve upon previous constructions of neural networks for a given convex CPWL function and apply our framework to obtain results in the nonconvex case.

3. 

   Veronese polytopes: Extending the framework of cyclic polytopes with Roland Púček. 2024. [abstract] [arXiv]

   This article introduces the theory of Veronese polytopes, a broad generalisation of cyclic polytopes. These arise as convex hulls of points on curves with one or more connected components, obtained as the image of the rational normal curve in affine charts. We describe their facial structure by extending Gale’s evenness condition, and provide a further combinatorial characterisation of facets via σ-parity alternating sequences. Notably, we establish a bijective correspondence between combinatorial types of Veronese polytopes and partitions of finite sets equipped with a cyclic order, called circular compositions. We show that, although the only Veronese 3-polytopes are the cyclic 3-polytopes and the octahedron, in general dimension they form a rich and diverse class including all combinatorial types of simplicial d-polytopes with at most d+3 vertices, the cross-polytope and particular stacked polytopes. In addition, we characterise which curves defining Veronese polytopes are d-order curves, and provide a closed formula for the number of facets of any Veronese polytope.

2024

1. 

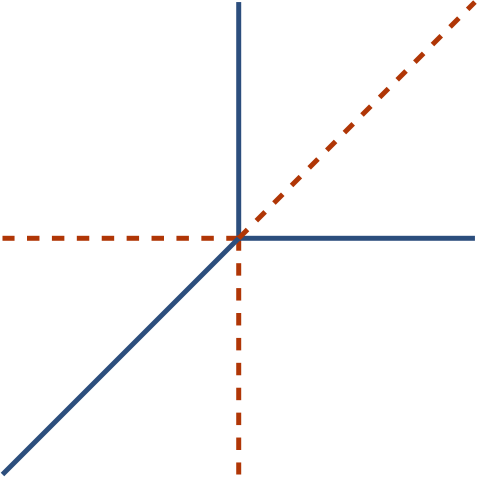
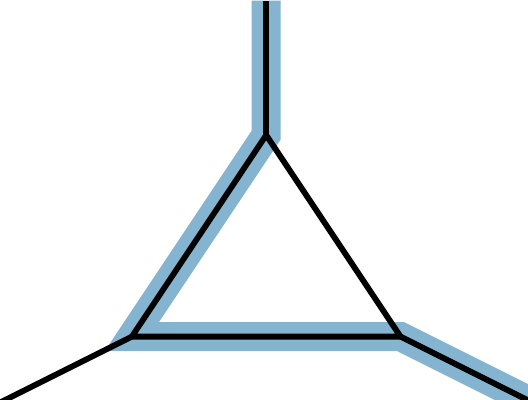
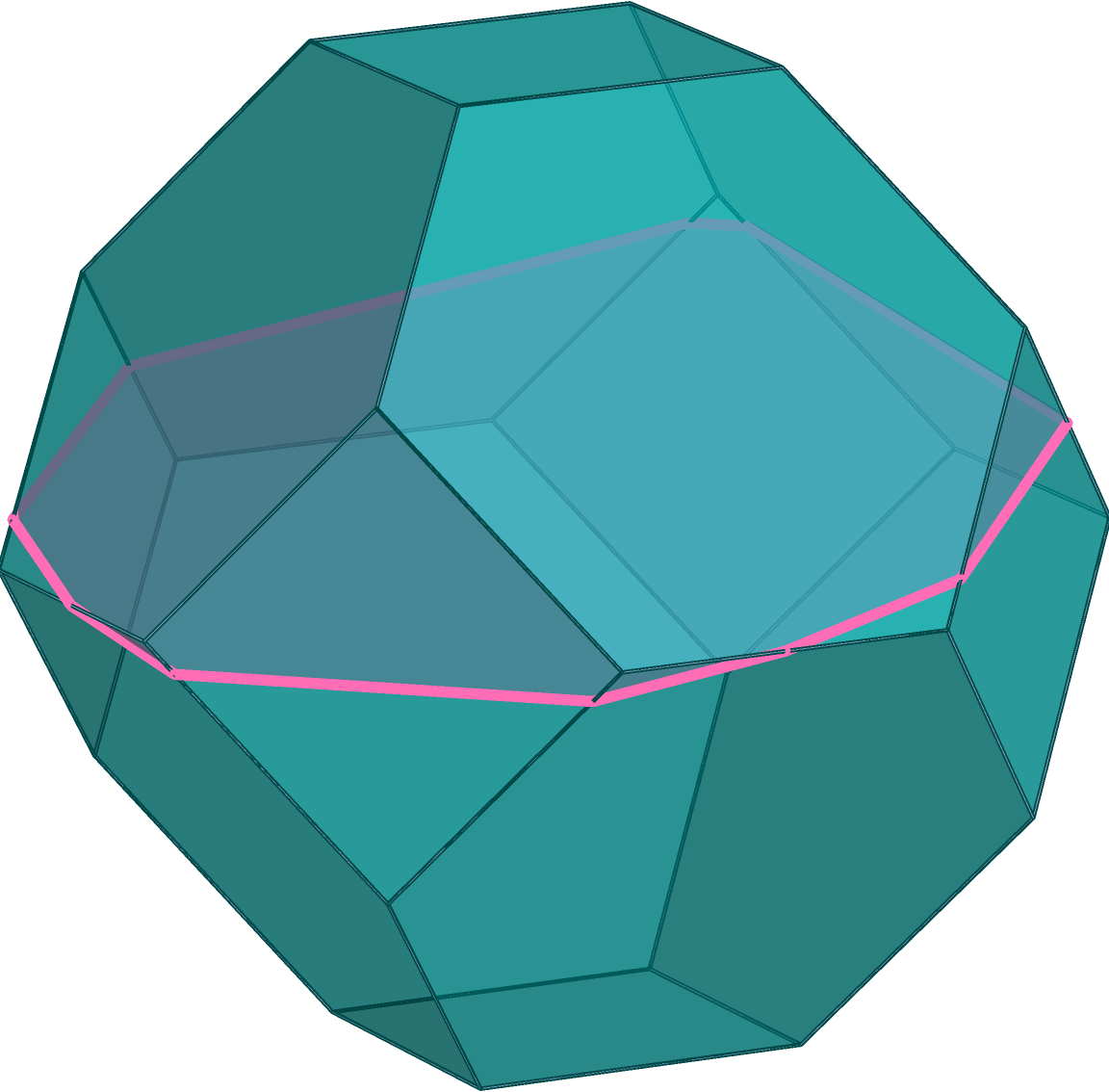
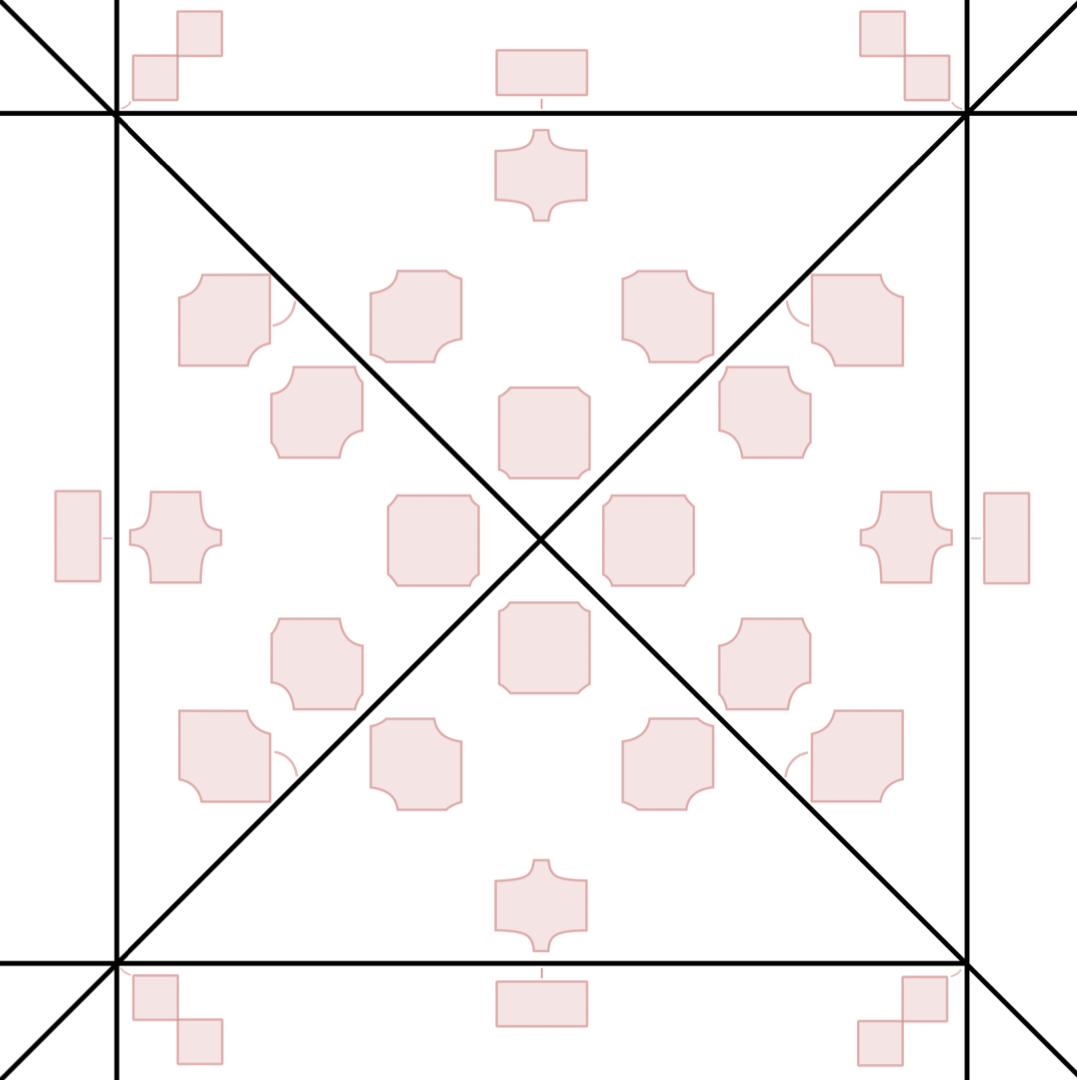
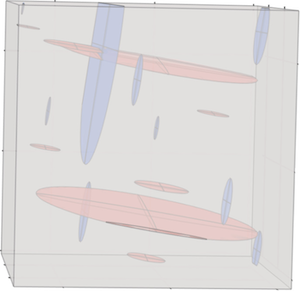
   The Real Tropical Geometry of Neural Networks for Binary Classification with Georg Loho, and Guido Montúfar. Transactions on Machine Learning Research, September 2024. [abstract] [url] [bibtex]

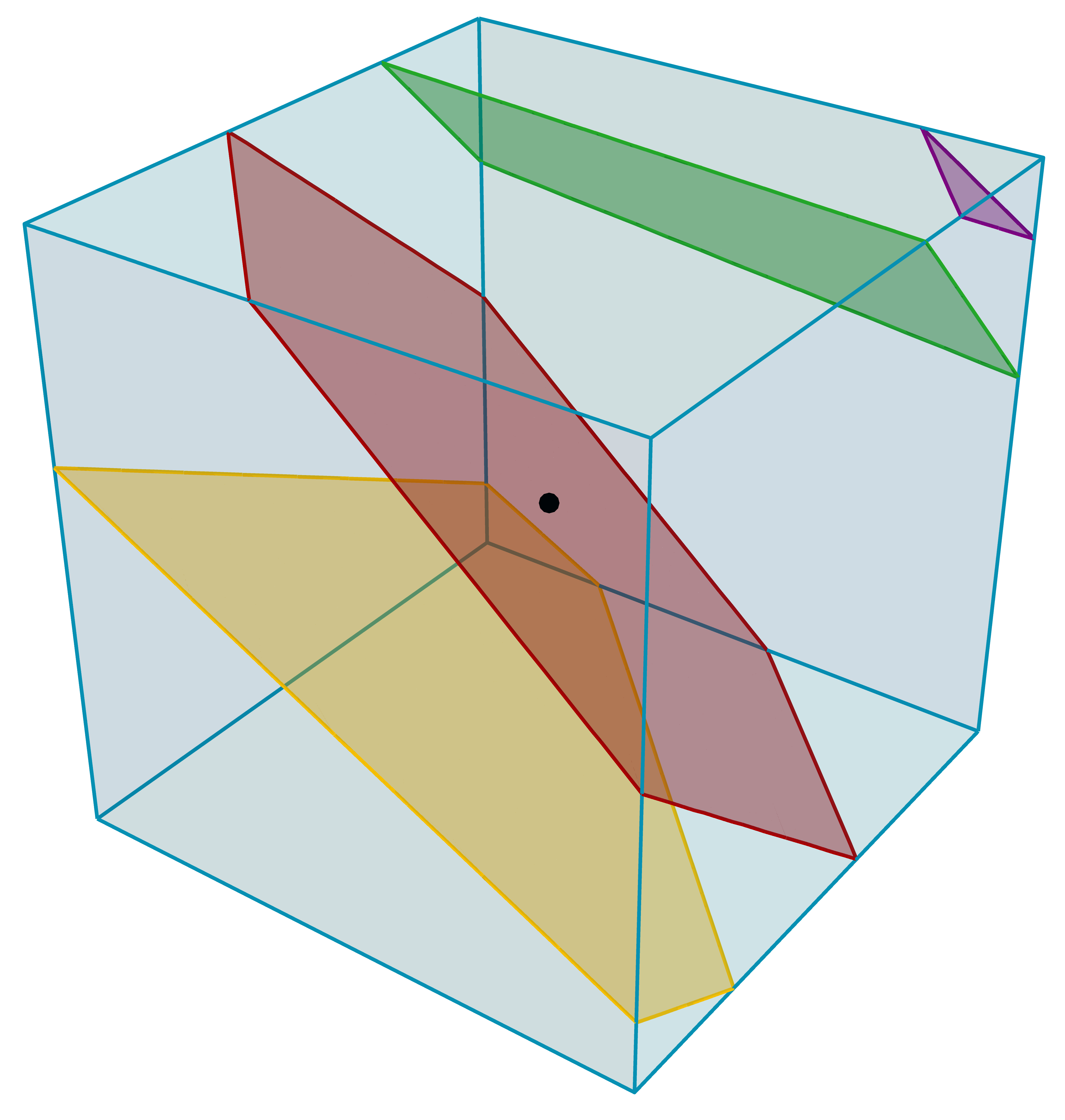
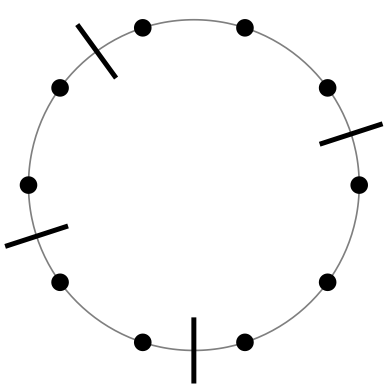
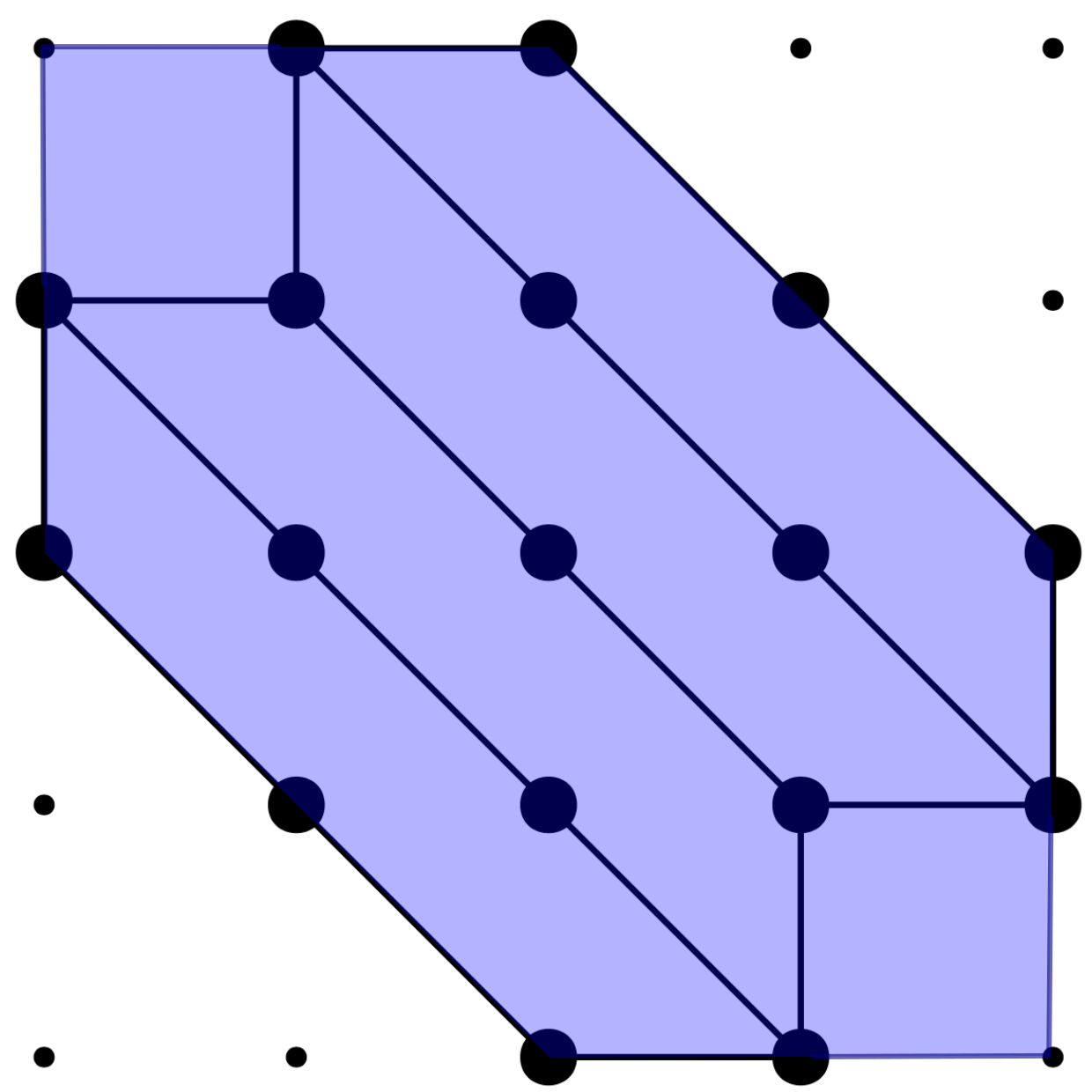
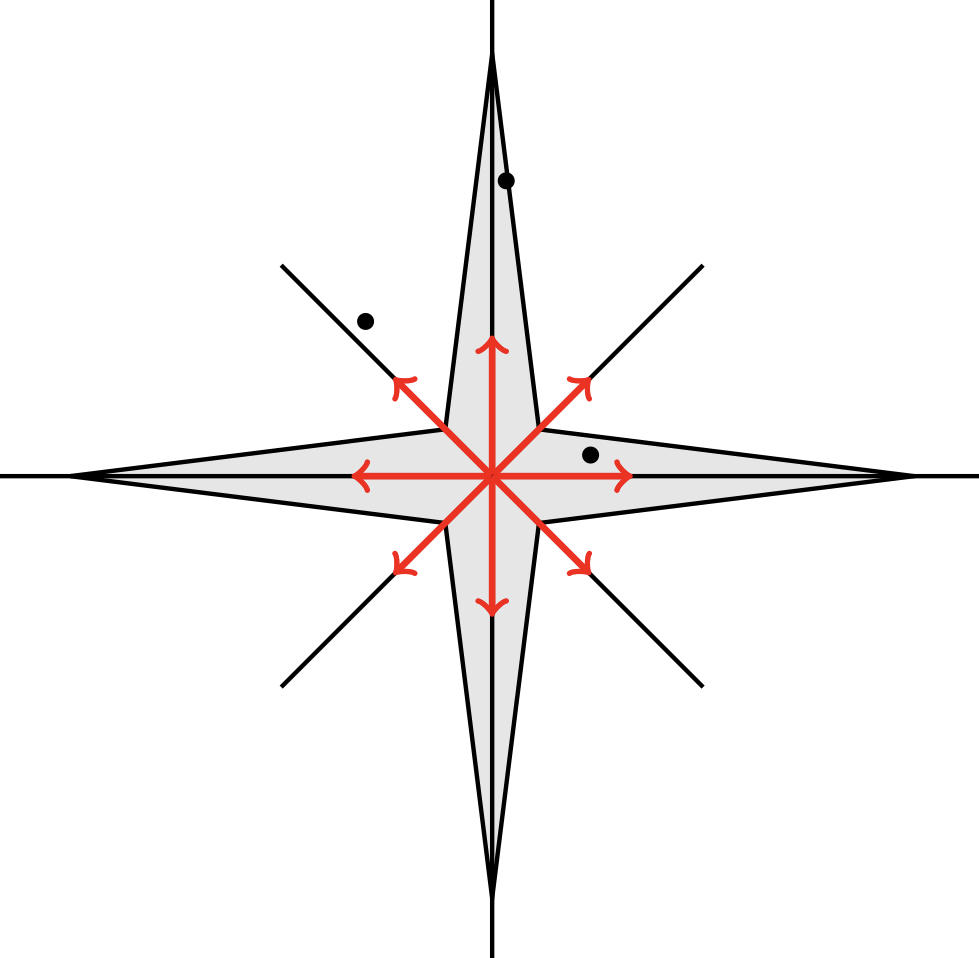
   We consider a binary classifier defined as the sign of a tropical rational function, that is, as the difference of two convex piecewise linear functions. In particular, the set of functions represented by a ReLU neural network can be regarded as a subset in the parameter space of tropical rational functions, specifically, it is contained as a semialgebraic set. We initiate the study of two different subdivisions of the parameter space of tropical rational functions with fixed number of terms in the numerator and denominator: a subdivision into semialgebraic sets, on which the combinatorial type of the decision boundary is fixed, and a subdivision into a polyhedral fan, capturing the combinatorics of the partitions of the dataset. The sublevel sets of the 0/1-loss function arise as subfans of this classification fan, and we show that the level-sets are not necessarily connected. We describe the classification fan i) geometrically, as normal fan of the activation polytope, and ii) combinatorially through a list of properties of associated bipartite graphs, in analogy to covector axioms of oriented matroids and tropical oriented matroids. Our findings extend and refine the connection between neural networks and tropical geometry by observing structures established in real tropical geometry, such as positive tropicalizations of hypersurfaces and tropical semialgebraic sets.

   @article{blm24,
     title = {The Real Tropical Geometry of Neural Networks for Binary Classification},
     author = {Brandenburg, Marie-Charlotte and Loho, Georg and Mont\'{u}far, Guido},
     journal = {Transactions on Machine Learning Research},
     year = {2024},
     month = sep,
     issn = {2835-8856},
     url = {https://openreview.net/forum?id=I7JWf8XA2w}
   }
   

2. 

   The Best Ways to Slice a Polytope with Jesús A. de Loera, and Chiara Meroni. Mathematics of Computation, 2024. [abstract] [doi] [arXiv] [supplementary material] [bibtex]

   We study the structure of the set of all possible affine hyperplane sections of a convex polytope. We present two different cell decompositions of this set, induced by hyperplane arrangements. Using our decomposition, we bound the number of possible combinatorial types of sections and craft algorithms that compute optimal sections of the polytope according to various combinatorial and metric criteria, including sections that maximize the number of \(k\)-dimensional faces, maximize the volume, and maximize the integral of a polynomial. Our optimization algorithms run in polynomial time in fixed dimension, but the same problems show hardness otherwise. Our tools can be extended to intersection with halfspaces and projections onto hyperplanes. Finally, we present several experiments illustrating our theorems and algorithms on famous polytopes.

   @article{bdlm24,
     title = {The Best Ways to Slice a Polytope},
     author = {Brandenburg, Marie-Charlotte and {de Loera}, Jes\'us A. and Meroni, Chiara},
     journal = {Mathematics of Computation},
     year = {2024},
     doi = {10.1090/mcom/4006}
   }
   

3. 

   Intersection Bodies of Polytopes: Translations and Convexity with Chiara Meroni. Journal of Algebraic Combinatorics, May 2024. [abstract] [doi] [bibtex]

   We continue the study of intersection bodies of polytopes, focusing on the behavior of \(IP\) under translations of \(P\). We introduce an affine hyperplane arrangement and show that the polynomials describing the boundary of \(I(P+t)\) can be extended to polynomials in variables \(t ∈R^d\) within each region of the arrangement. In dimension 2, we give a full characterization of those polygons such that their intersection body is convex. We give a partial characterization for general dimensions.

   @article{bm24,
     title = {Intersection Bodies of Polytopes: Translations and Convexity},
     author = {Brandenburg, Marie-Charlotte and Meroni, Chiara},
     year = {2024},
     month = may,
     journal = {Journal of Algebraic Combinatorics},
     doi = {10.1007/s10801-024-01328-9}
   }
   

4. 

   Combinatorics of Correlated Equilibria with Benjamin Hollering, and Irem Portakal. Experimental Mathematics, April 2024. [abstract] [doi] [supplementary material] [bibtex]

   We study the correlated equilibrium polytope \(P_G\) of a game \(G\) from a combinatorial point of view. We introduce the region of full-dimensionality for this class of polytopes and prove that it is a semialgebraic set for any game. Using a stratification via oriented matroids, we propose a structured method for describing the possible combinatorial types of \(P_G\), and show that for \((2 \times n)\)-games, the algebraic boundary of the stratification is a union of coordinate hyperplanes and binomial hypersurfaces. Finally, we provide a computational proof that there exists a unique combinatorial type of maximal dimension for generic \((2 \times 3)\)-games.

   @article{bhp24,
     title = {Combinatorics of Correlated Equilibria},
     author = {Brandenburg, Marie-Charlotte and Hollering, Benjamin and Portakal, Irem},
     journal = {Experimental Mathematics},
     year = {2024},
     month = apr,
     doi = {10.1080/10586458.2024.2340000}
   }
   

2023

1. 

   Tropical Positivity and Determinantal Varieties with Georg Loho, and Rainer Sinn. Algebraic Combinatorics, 6(4):999–1040, August 2023. [abstract] [doi] [bibtex]

   We initiate the study of positive-tropical generators as positive analogues of the concept of tropical bases. Applying this to the tropicalization of determinantal varieties, we develop criteria for characterizing their positive part. We focus on the study of low-rank matrices, in particular matrices of rank 2 and 3. Moreover, in the case square-matrices of corank 1, we fully classify the signed tropicalization of the determinantal variety, even beyond the positive part.

   @article{bls23,
     title = {Tropical Positivity and Determinantal Varieties},
     author = {Brandenburg, Marie-Charlotte and Loho, Georg and Sinn, Rainer},
     journal = {Algebraic Combinatorics},
     pages = {999--1040},
     publisher = {The Combinatorics Consortium},
     volume = {6},
     number = {4},
     year = {2023},
     month = aug,
     doi = {10.5802/alco.286}
   }
   

2. 

   Competitive equilibrium always exists for combinatorial auctions with graphical pricing schemes with Christian Haase, and Ngoc Mai Tran. La Matematica, 2:1–30, March 2023. [abstract] [doi] [bibtex]

   We show that a competitive equilibrium always exists in combinatorial auctions with anonymous graphical valuations and pricing, using discrete geometry. This is an intuitive and easy-to-construct class of valuations that can model both complementarity and substitutes, and to our knowledge, it is the first class besides gross substitutes that have guaranteed competitive equilibrium. We prove through counter-examples that our result is tight, and we give explicit algorithms for constructive competitive pricing vectors. We also give extensions to multi-unit combinatorial auctions (also known as product-mix auctions). Combined with theorems on graphical valuations and pricing equilibrium of Candogan, Ozdagar and Parrilo, our results indicate that quadratic pricing is a highly practical method to run combinatorial auctions.

   @article{bht23,
     title = {Competitive equilibrium always exists for combinatorial auctions with graphical pricing schemes},
     author = {Brandenburg, Marie-Charlotte and Haase, Christian and Tran, Ngoc Mai},
     year = {2023},
     month = mar,
     doi = {10.1007/s44007-022-00038-7},
     journal = {La Matematica},
     volume = {2},
     pages = {1--30}
   }
   

3. 

   Multivariate volume, Ehrhart, and \(h^*\)-polynomials of polytropes with Sophia Elia, and Leon Zhang. Journal of Symbolic Computation, 114:209-230, January 2023. [abstract] [doi] [supplementary material] [bibtex]

   The univariate Ehrhart and \(h^*\)-polynomials of lattice polytopes have been widely studied. We describe methods from toric geometry for computing multivariate versions of volume, Ehrhart and \(h^*\)-polynomials of lattice polytropes, which are both tropically and classically convex. These algorithms are applied to all polytropes of dimensions 2,3 and 4, yielding a large class of integer polynomials. We give a complete combinatorial description of the coefficients of volume polynomials of 3-dimensional polytropes in terms of regular central subdivisions of the fundamental polytope. Finally, we provide a partial characterization of the analogous coefficients in dimension 4.

   @article{bez23,
     title = {Multivariate volume, Ehrhart, and \(h^*\)-polynomials of polytropes},
     author = {Brandenburg, Marie-Charlotte and Elia, Sophia and Zhang, Leon},
     journal = {Journal of Symbolic Computation},
     volume = {114},
     pages = {209-230},
     year = {2023},
     month = jan,
     issn = {0747-7171},
     doi = {10.1016/j.jsc.2022.04.011}
   }
   

2022

1. 

   Extended Abstract: Competitive equilibrium always exists for combinatorial auctions with graphical pricing schemes with Christian Haase, and Ngoc Mai Tran. In: L. F. Tabera Alonso (ed.), Discrete Mathematics Days 2022, pp. 64–70, June 2022. [doi] [pdf] [bibtex]

   @inproceedings{bht22,
     author = {Brandenburg, Marie-Charlotte and Haase, Christian and Tran, Ngoc Mai},
     booktitle = {Discrete Mathematics Days 2022},
     title = {Extended Abstract: Competitive equilibrium always exists for combinatorial auctions with graphical pricing schemes},
     year = {2022},
     editor = {{L. F. Tabera Alonso}},
     month = jun,
     pages = {64--70},
     publisher = {Editorial Universidad de Cantabria, Santander},
     doi = {10.22429/Euc2022.016},
     isbn = {978-84-19024-03-9},
     pdf = {https://dmd2022.unican.es/978-84-19024-03-9.pdf}
   }
   

2. 

   Intersection Bodies of Polytopes with Katalin Berlow, Chiara Meroni, and Isabelle Shankar. Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry, 63(2):419–439, June 2022. [abstract] [doi] [supplementary material] [bibtex]

   We investigate the intersection body of a convex polytope using tools from combinatorics and real algebraic geometry. In particular, we show that the intersection body of a polytope is always a semialgebraic set and provide an algorithm for its computation. Moreover, we compute the irreducible components of the algebraic boundary and provide an upper bound for the degree of these components.

   @article{bbms22,
     title = {Intersection Bodies of Polytopes},
     author = {Berlow, Katalin and Brandenburg, Marie-Charlotte and Meroni, Chiara and Shankar, Isabelle},
     year = {2022},
     month = jun,
     journal = {Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry},
     volume = {63},
     number = {2},
     pages = {419--439},
     doi = {10.1007/s13366-022-00621-7}
   }
   

2021

1. 

   Investigation of hydro-mechanical processes in fluid-saturated fractured rock based on numerical model generation with Nele Pollmann, Julia Gallas, Lucas Witte, and Tobias Backers. IOP Conference Series: Earth and Environmental Science, 833(1):012107, August 2021. [abstract] [doi] [bibtex]

   To realistically simulate fluid flow in fractured rock mass, a scheme to represent the discrete fracture networks (DFN) in the numerical model is of utmost importance. In this paper we discuss a workflow to implement a field-measurement based DFN into an FEM code (COMSOL Multiphysics) by means of a MATLAB routine. This workflow is involved in the ZoKrateS project which aims at showing the feasibility to enhanced fractured carbonate Rock Mass by proppant placement for geothermal application. The model generation is based on analytical geometry including the equations for dip, azimuth and spacing of lines. The spacing between the discontinuities and the characteristic fracture length and aperture as well as orientation serve as input parameters for the model. It is possible to generate periodic models to be able to include periodic boundary conditions in simulations. In 2D the fractures are modeled as poroelastic ellipses in a poroelastic square- matrix. We investigate hydro-mechanically triggered fluid transport in stationary fractures that are mechanically and hydraulically active. An extension to 3D fracture networks requires an algorithm based on analytical geometry including the equations for azimuth, dip and spacing of planes. To decrease the numerical costs of the 3D simulation a diffuse interface approach is strived for, including a modified model generation. With the numerical model generator (NUMOG) a workflow is developed which allows numerical investigations of (thermo-) hydro-mechanically triggered fluid transport in a geothermal reservoir.

   @article{pgbwb21,
     title = {Investigation of hydro-mechanical processes in fluid-saturated fractured rock based on numerical model generation},
     author = {Pollmann, Nele and Gallas, Julia and Brandenburg, Marie-Charlotte and Witte, Lucas and Backers, Tobias},
     year = {2021},
     month = aug,
     number = {1},
     pages = {012107},
     volume = {833},
     doi = {10.1088/1755-1315/833/1/012107},
     publisher = {{IOP} Publishing},
     journal = {{IOP} Conference Series: Earth and Environmental Science}
   }
   

2023

1. 

   PhD Thesis: Tropical Positivity and Semialgebraic Sets from Polytopes Advisor: Rainer Sinn, 2023. [url] [slides]

2019

1. 

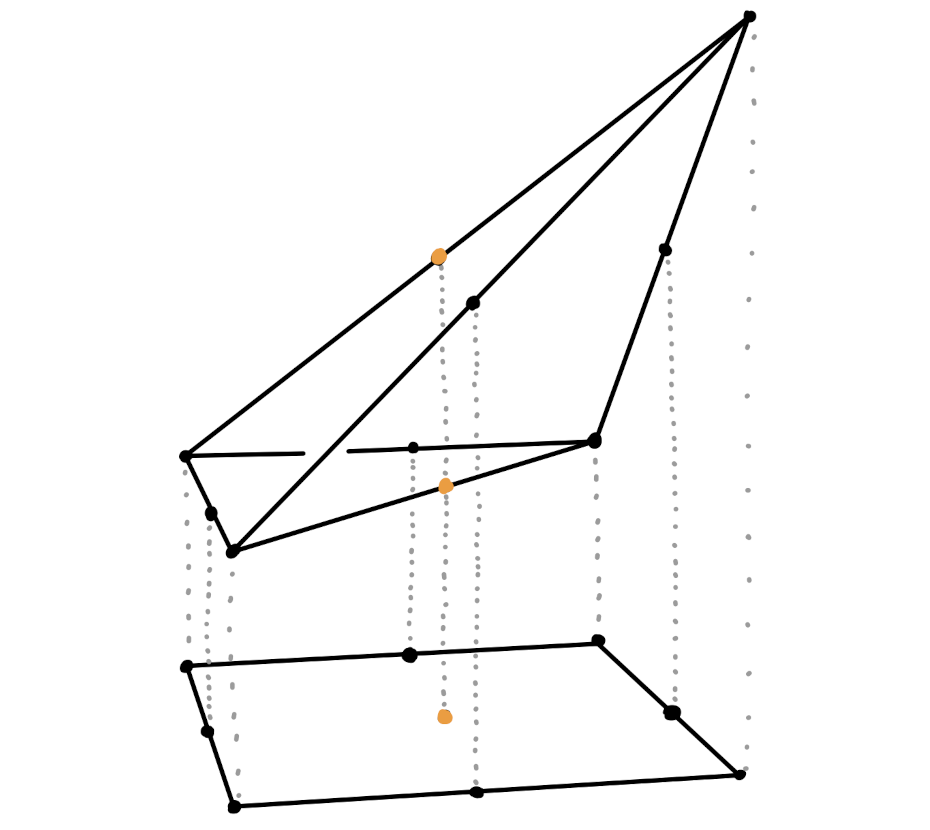   Master Thesis: Competitive Equilibrium and Lattice Polytopes Advisor: Christian Haase, 2019. [abstract]

   A competitive equilibrium is an envy-free allocation of goods. That is, given a price function that assigns a nonnegative value to each bundle of items, each agent prefers the allocated bundle to every other affordable bundle of goods, or is indifferent towards them. It is further required that the allocation clears the market, i.e. each item is allocated to exactly one agent. There is a particular interest in economics in conditions on the existence of a competitive equilibrium for indivisible goods. In a recent work, Condogan et al. study such conditions in the setting of graphical valuations, which is a class of valuations associated to a value graph, whose nodes correspond to items and whose edges encode (pairwise) complementarities or substitutabilities between items. We explore a connection between these graphical valuations and regular subdivisions of a polytope that can be constructed from the value graph. We show that a competitive equilibrium exists for all sets of valuations and any bundle of indivisible goods, provided that, in the setting of anonymous graphical pricing, the value graphs of all agents correspond to complete graphs.

2016

1. 

   Bachelor Thesis: A 4-Simple 4-Simplicial 8-Polytope Advisor: Günter M. Ziegler, 2016. [abstract]

   The Gosset polytope 2_41 is - besides the simplices of dimension 4 and higher - the only 4-simple, 4-simplicial polytope known to date. We discuss its construction via the Wythoff construction and the underlying reflection group E8. We also consider the exceptional root system E8 and the fundamental properties of the polytope: 4-simplicity, 4-simplicialty and its f-vector.